近期，中国科学院上海天文台研究人员通过理论推导，深入分析了处于旋转自引力平衡的椭球Boussinesq流体中的热不稳定性问题，首次得到快速旋转椭球形天体内部流体热不稳定性的判据，这一理论不仅可以直接用于理解木星与土星这样显著非球形行星内部的对流动力学，甚至可能被用于研究黑洞吸积盘等极端扁平的旋转流体系统。相关研究成果于10月27日发表在流体力学期刊Physical Review Fluids上，并被美国物理学会（American Physical Society）选为媒体推荐成果。 

　　热对流运动是天体内部普遍存在的动力学现象，对能量传递、物质输运、磁场产生和演化路径起到支配性的作用。如果一个天体没有自转，可以简单地依据实际温度梯度和绝热温度梯度之间的比较来判断该天体内部是否发生热对流。但实际上，行星与恒星总是自转的，科里奥利力（即地转偏向力）破坏了对流方程的SO(3)对称性，导致动力系统的临界特性完全改变^[1]。 

　　钱德拉塞卡（S. Chandrasekhar）最早分析旋转球形流体的热不稳定性判据^[2]。几十年以来，众多学者系统性地研究了球形近似条件下流体从传导态到对流态复杂的线性分岔性质^[3-11]。迄今为止，以上所有研究都忽略了天体由于自转产生的离心力而形成的非球形形状，因此这一系列基于球形近似条件所获得的研究结论的合理性和有效性从未得到任何理论或数值分析的检验。但随着人们对木星、土星和α Eridani等快速自转天体观测和研究的不断加深，椭球形天体内部全局热不稳定性判据变得愈发必要^[12-14]。 

　　在快速旋转非球形稳定分层模型的基础上^[15]，中国科学院上海天文台行星物理与磁流体力学课题组孔大力研究员指导澳门科技大学月球与行星科学国家重点实验室博士研究生李文博，运用全局渐进展开的分析手段深入分析了处于旋转自引力平衡的椭球Boussinesq流体中的热不稳定性问题，首次获得了全局热对流线性临界模式和临界参数的解析解，并系统地探讨了非球形形状与对流动力学分岔性质之间的联系。（图1：以木星的扁率情况为例，展示了全局热不稳定性发生时的临界对流模式。） 

　　“研究结果证明，对于像木星这样的快速自转且扁率较大的行星，非球形旋转对流的临界参数与球形近似下的结果相比，会出现大幅度变化。”孔大力研究员表示，“如果严格采用与天体自转相自洽的非球形模型，很多快速自转行星与恒星内部的对流输运效率会与前人的预期相差很大。”他还指出，这一研究成果对天体热演化、磁场发电机动力学等问题的影响将在后续同一系列的学术论文中深入探讨。 

　　本研究获得国家自然科学基金面上项目、中国科学院B类战略性先导科技专项，以及国家国防科技工业局民用航天技术预先研究项目等的资助。 

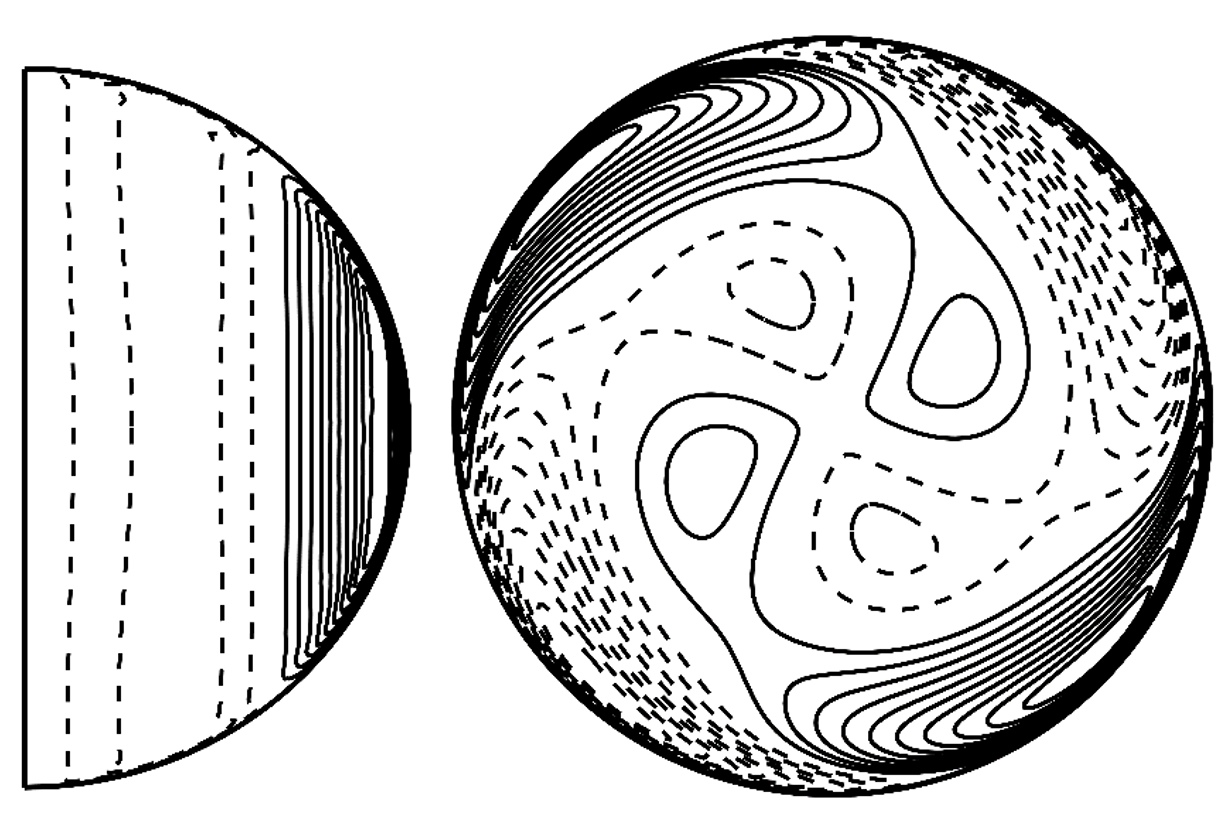
图1，以埃克曼数E=0.0001、普朗特数Pr=0.005时、弗罗德数Fr=0.05的参数情况为例，全局渐进理论预期麦克劳林椭球流体内线性热不稳定性模式是经度方向波数为2的准地转波。这与三维数值模拟得到的子午面（左图）和赤道面（右图）中对流的结构完全吻合。 

参考文献： 

[1] K. Zhang and G. Schubert, Magnetohydrodynamics in rapidly rotating spherical systems, Annual Review of Fluid Mechanics 32, 409 (2000). 

[2] S. Chandrasekhar, Hydrodynamic and Hydromagnetic Stability (Clarendon Press, Oxford, 1962). 

[3] P. H. Roberts, On the thermal instability of a rotating-fluid sphere containing heat sources, Philosophical Transactions of the Royal Society of London. Series A 263, 93 (1968). 

[4] F. Busse, Thermal instabilities in rapidly rotating systems, Journal of Fluid Mechanics 44, 441 (1970). 

[5] A. M. Soward, On the finite amplitude thermal instability of a rapidly rotating fluid sphere, Geophysical and Astrophysical Fluid Dynamics 9, 19 (1977). 

[6] J.-I. Yano, Asymptotic theory of thermal convection in rapidly rotating systems, Journal of Fluid Mechanics 243, 103 (1992). 

[7] K. Zhang, On coupling between the Poincaré equation and the heat equation, Journal of Fluid Mechanics 268, 211 (1994). 

[8] K. Zhang, On coupling between the Poincaré equation and the heat equation: non-slip boundary condition, Journal of Fluid Mechanics 284, 211 (1995). 

[9] C. A. Jones, A. W. Soward, and A. I. Mussa, The onset of thermal convection in a rapidly rotating sphere, Journal of Fluid Mechanics 405, 157 (2000). 

[10] E. Dormy, A. M. Soward, and C. A. Jones, The onset of thermal convection in rotating spherical shells, JFM 501, 43 (2004). 

[11] J. Sánchez Umbría and M. Net, Continuation of double Hopf points in thermal convection of rotating fluid spheres, SIAM Journal on Applied Dynamical Systems 20, 208 (2021). 

[12] D. Kong, K. Zhang, G. Schubert, and J. D. Anderson, Origin of Jupiter’s cloud-level zonal winds remains a puzzle even after Juno, PNAS 155, 8499 (2018). 

[13] P. Kervella, A. Domiciano de Souza, S. Kanaan, and et al., The environment of the fast rotating star Achernar ii. Thermal infrared interferometry with VLTI/MIDI, A&A 493, L53 (2009). 

[14] A. Maeder, C. Georgy, and D. Meynet, Convective envelopes in rotating OB stars, A&A 479, L37 (2008). 

[15] D. Kong, Rapidly rotating self-gravitating Boussinesq fluid: A non-spherical model of motionless stable stratification, Physical Review Fluids 7, 074803 (2022). 

论文链接：https://link.aps.org/doi/10.1103/PhysRevFluids.7.103502 

科学联系人：